PyWavelets可能是迄今最强大的Python小波变换库
小波变换(WT), 也称为小波分析,是解决傅里叶变换 (FT) 缺点的最新解决方案。 小波变换(WT)在把信号周期(或频率)转换时,不会失去时间分辨率。 在信号处理方面,它提供了一种方法,把感兴趣的输入信号分解一系列的解基本的波形,即"小波"., 然后,通过检查这些小波基的系数(或权重),分析信号。
1. 小波变换的应用
小波变换可用于平稳和非平稳信号,包括但不限于以下几方面:
- 信号除噪
- trend analysis and forecasting
- 检测数据中的突然、不连续、变化或异常行为等
- 压缩大数据
- 如JPEG2000的新图像压缩标准完全基于小波
- 数据加密,即数据安全
- 与机器学习相结合,提高建模精度
2. PyWavelets
PyWavelets库 是一个开源Python小波变换库,它是在麻省理工学院许可证下发布。
PyWavelets的主要特点是,它可以对1D、2D和nD信号进行小波变换,其包括以下主要变换:
- 单层离散小波变换和反离散小波变换(DWT和IDWT)
- 多层次离散小波变换和反向重构
- 平稳小波变换(非抽取小波变换)
- 小波包分解和重建
- 连续小波变换
- 多分辨率分析(MRA)
3. 安装PyWavelets和需要的软件包
PyWavelets has dropped support for Python 3.5 and 3.6 and now supports Python 3.7–3.10. PyWavelets is only dependent on NumPy (supported versions are currently >= 1.14.6). Besides, Matplotlib are required for visualization.
从PyPI:
pip install PyWavelets matplotlibFor Anaconda Users, Anaconda has these packages installed. If you have not installed it on your PC, you can install by:
conda install -c conda-forge pywavelets matplotlib4. Built-in Wavelet Families and Family Members
One can simply check and display all PyWavelets Built-in Wavelet Families and their members using the following command:
import pywtfor family in pywt.families():print(f'{family} family: {pywt.wavelist(family)}')
然后它返回的一个如下列表:

5. 近似小波和尺度函数图像
5.1. 导入所需的软件包
# import the required packages
import pywt
import matplotlib.pyplot as plt5.2 离散小波函数和尺度函数图像
(1)正交小波
首先,获得给定小波的近似函数和尺度函数,例如,采取'db5'和'level=1'。
wavelet = pywt.Wavelet('db5')[phi, psi, x] = wavelet.wavefun(level=1)绘制小波函数图:
plt.plot(x,psi)plt.show()输出以下图像:
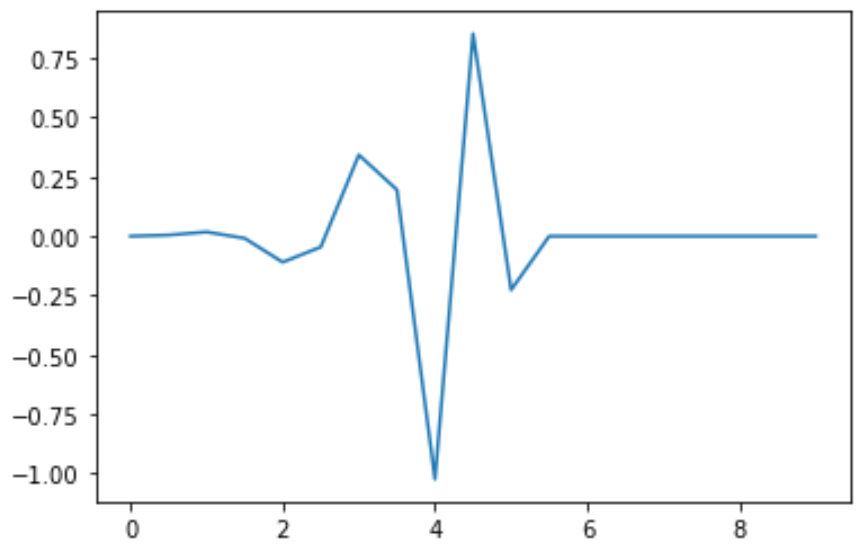
尺度函数图像:
plt.plot(x,phi)
plt.show()结果如下:
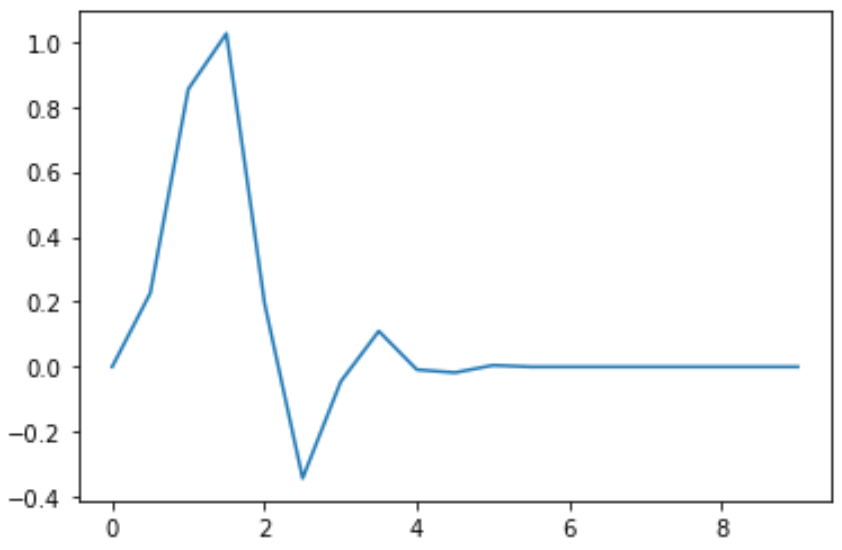
(2)其他小波
For other (biorthogonal but not orthogonal) wavelets, it returns approximations of scaling function and wavelet function both for decomposition and reconstruction and corresponding x-grid coordinates.
例如,小波'bior3.5',level=5的分解和重构值尺度函数和近似小波函数:
biwavelet = pywt.Wavelet('bior3.5')
[phi_d,psi_d,phi_r,psi_r,x] = biwavelet.wavefun(level=5)他们的图像代码如下:
# Wavelet Function of decomposition
plt.plot(x,psi_d)
plt.show()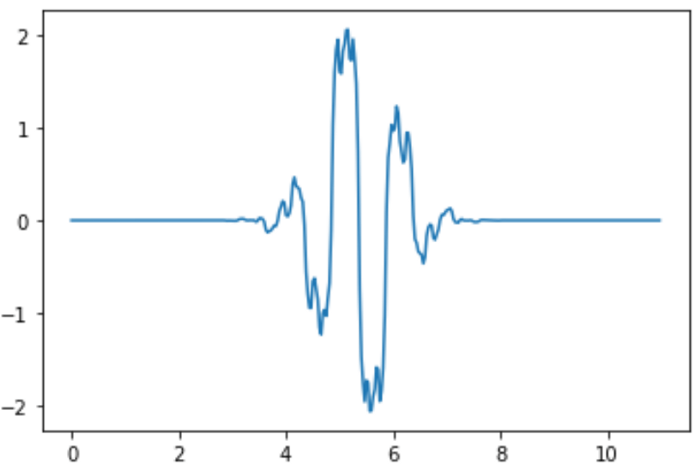
图 3. 小波'bior3.5' 5阶小波分解函数的图像
# wavelet function of reconstruction
plt.plot(x,psi_r)
plt.show()
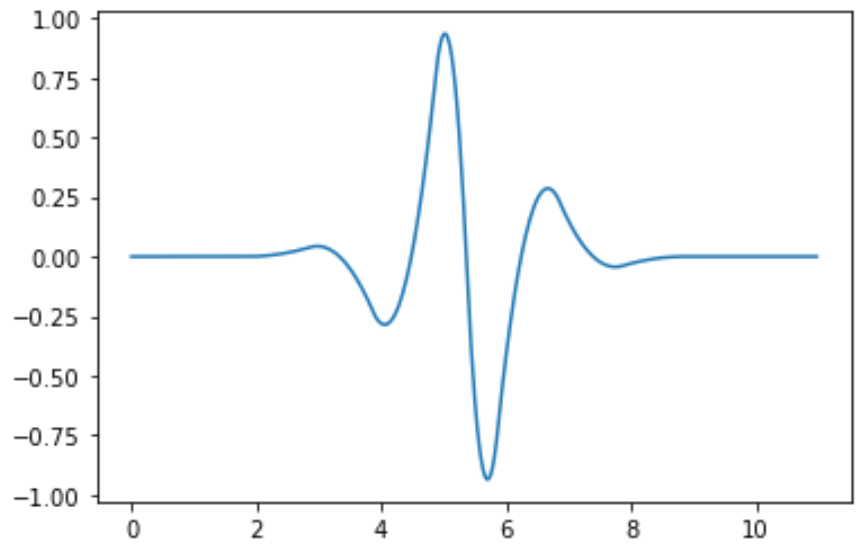
图4. 小波'bior3.5' 5阶小波重构函数的图像
# scaling functions of decomposition
plt.plot(x,phi_d)
plt.show()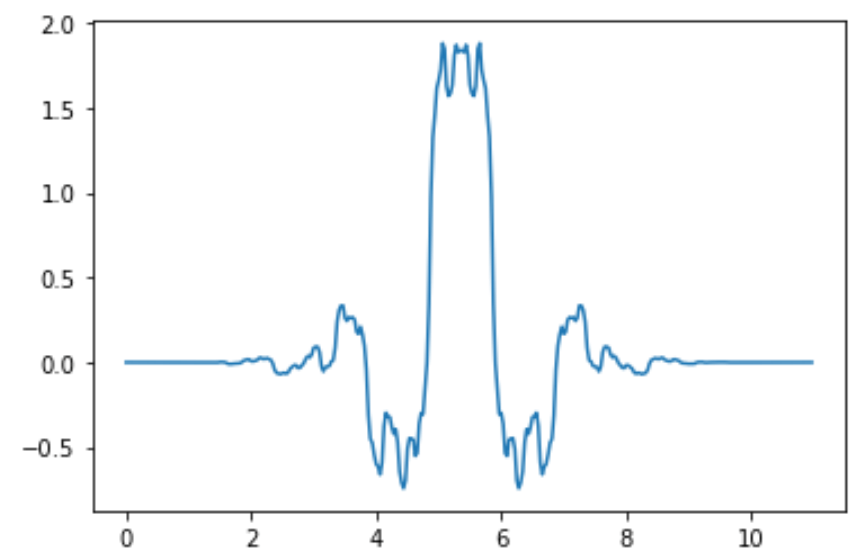
# Scaling function of reconstruction
plt.plot(x,phi_r)
plt.show()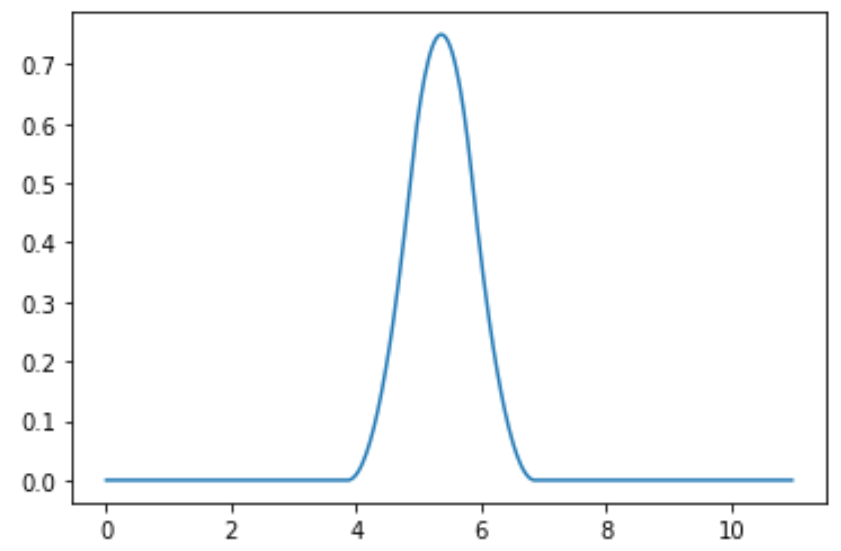
5.3. 连续小波函数
我们采取'gaus2' 5阶小波举例如下:
(1)获得近似小波函数
W = pywt.ContinuousWavelet(‘gaus2’)
[psi,x] = Wavelet.wavefun(level=5)(2)绘制小波函数图
plt.plot(x,psi)
plt.show()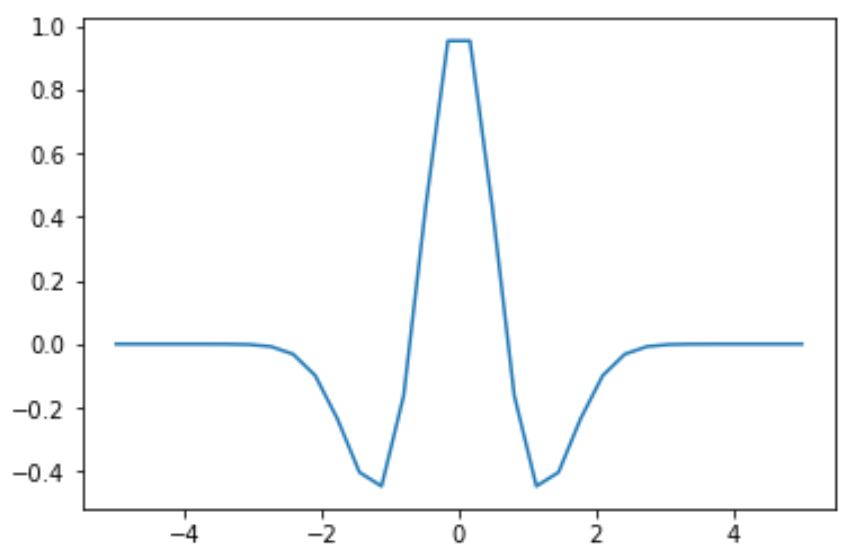
5.4. 在线课程
If you are interested in learning Practical Wavelet Transforms from the very beginning, welcome to my online course via the following linage:
