使用Python绘制离散小波滤波器组的图像

滤波器法是一种有效方式，来实施离散波变换。

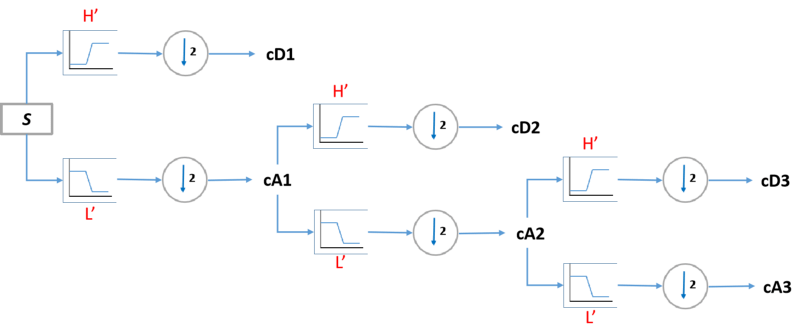
1. 什么是滤波器组

滤波器组在现代信号和图像处理方面发挥着重要作用。 正如其名称所示，滤波器组是一组过滤器，意思是说一系列过滤器，或者说许多过滤器，而每个滤波器都应用于原始信号。 因此，一个信号可以分解成2个或更多的信号。 那么什么是滤波器组？

Simply speaking, a Filter Bank can be defined as a system (an array) of bandpass filters  that split the input signal (S_t)拆分为分析信号(x_1t, x_2t, ..., x_nt )和每一个分析信号都是原始信号某频率子频段。

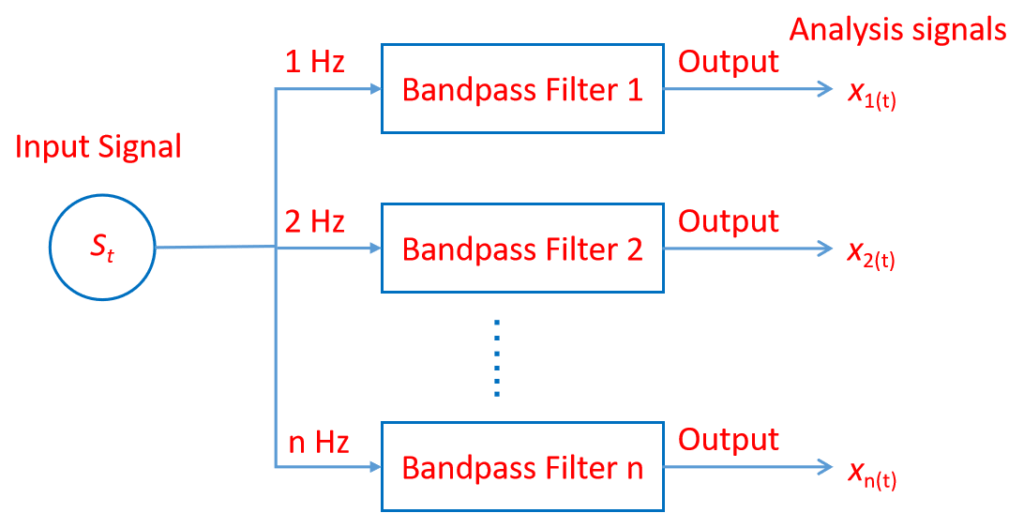
在小波分析中滤滤器组通常是指产生小波尺度函数和小波基函数的体系。 上图显示了一个滤波器组的简单结构。

在实践中，有效实施离散小波变换(DWT)的方式就是使用滤波器组。该方法在1988年由Mallat提出， 这个非常实用的过滤算法便产生了快速离散小波变换(FWT).

2. 小波滤波器系数

小波滤波器系数是离散小波变换(DWT)中最重要的信息。 在Python PyWavelets库中，小波滤波器系数可以通过 dec_lo, dec_hi, rec_lo 和 rec_hi： 属性获得，其分别对应 低通 和 高通 分解滤波器 和 低通 和 高通 重构滤波器 。

前 面的文章曾经讨论过PyWavelets，它的安装，以及其内置小波族及其成员等等。 在PyWavelets， filter_bank法返回当前小波滤波器列表的顺序如下： [dec_lo,dec_hi,rec_lo,rec_hi].

• dec_lo：分解低通滤波器
• dec_hi：分解高通过滤器
• rec_lo：重构低通滤波器
• rec_hi：重构高通过滤器

3. 离散小波滤波器组的输出

首先，我们导入所需的软件包：一个是PyWavelets，另一个是进行可视化的matplotlib。

#导入所需的软件包
import pywt
import matplotlib.pyplot as plt

接下来，我们选取一个离散小波，例如，"db5"。然后显示其滤波器组如下：

wavelet = pywt.Wavelet('db5')
wavelet.filter_bank

输出如下：

([0.0033357252854737712,
  -0.012580751999081999,
  -0.006241490212798274,
  0.07757149384004572,
  -0.032244869584638375,
  -0.24229488706638203,
  0.13842814590132074,
  0.7243085284377729,
  0.6038292697971896,
  0.16010239797419293],
 [-0.16010239797419293,
  0.6038292697971896,
  -0.7243085284377729,
  0.13842814590132074,
  0.24229488706638203,
  -0.032244869584638375,
  -0.07757149384004572,
  -0.006241490212798274,
  0.012580751999081999,
  0.0033357252854737712],
 [0.16010239797419293,
  0.6038292697971896,
  0.7243085284377729,
  0.13842814590132074,
  -0.24229488706638203,
  -0.032244869584638375,
  0.07757149384004572,
  -0.006241490212798274,
  -0.012580751999081999,
  0.0033357252854737712],
 [0.0033357252854737712,
  0.012580751999081999,
  -0.006241490212798274,
  -0.07757149384004572,
  -0.032244869584638375,
  0.24229488706638203,
  0.13842814590132074,
  -0.7243085284377729,
  0.6038292697971896,
  -0.16010239797419293])

可以只输出某一个滤波器，如分解低通过滤器。可使用以下命令：

wavelet.dec_lo

得到以下结果：

[0.0033357252854737712,
 -0.012580751999081999,
 -0.006241490212798274,
 0.07757149384004572,
 -0.032244869584638375,
 -0.24229488706638203,
 0.13842814590132074,
 0.7243085284377729,
 0.6038292697971896,
 0.16010239797419293]

5. 小波滤波器组可视化

第一，获得四个滤波器的方法如下：

[dec_lo, dec_hi, rec_lo, rec_hi] = wavelet.filter_bank

Then, we can use Matplotlib to make a stem plot for each filter.

fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, figsize=(15,7))

ax1.stem(dec_lo) 
ax1.set_title('Decomposition low-pass filter')
ax2.stem(dec_hi)
ax2.set_title('Decomposition high-pass filter')
ax3.stem(rec_lo)
ax3.set_title('Reconstruction low-pass filter')
ax4.stem(rec_hi)
ax4.set_title('Reconstruction high-pass filter')

plt.savefig('./results/filter_bank.png') # save it in any path, here I save it into the results folder in the working directory
plt.show()

输出显示如下：

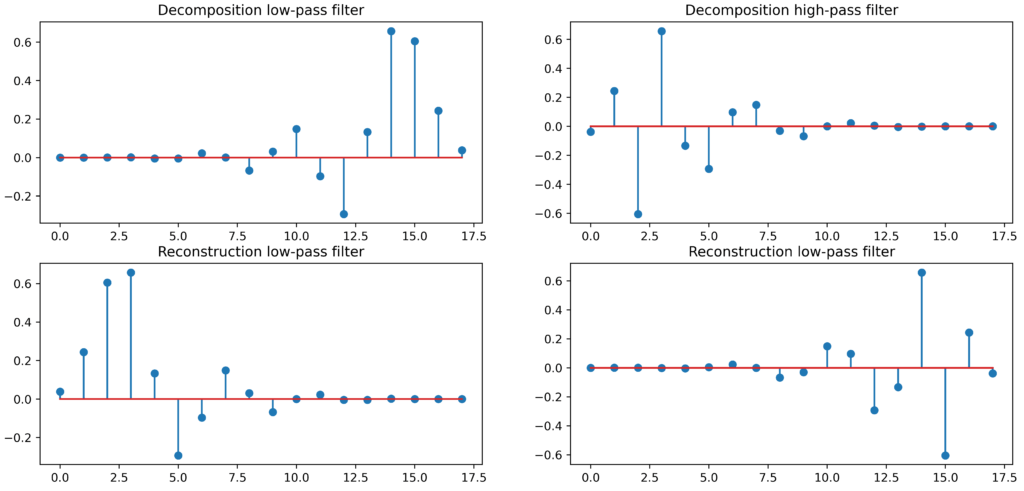
6. 在线课程

如果你有兴趣从基础学习实用小波变换，欢迎参加以下课程:

实用 Python 小波变换(I)：基础知识

实用Python小波变换(II)：一维离散小波变换