小波变换(WT), 也称为小波分析,是解决傅里叶变换 (FT) 缺点的最新解决方案。 小波变换(WT). WT transforms a signal in period (or frequency) without losing time resolution. In the signal processing context, WT provides a method to decompose an input signal of interest into a set of elementary waveforms, i.e. “wavelets”., and then analyze the signal by examining the coefficients (or weights) of these wavelets. In this post, we will introduce where the wavelet transforms can be used.
1. 小波变换的应用
在一般情况下,小波变换可以用于静止和非静态的信号,包括但不限于以下内容:
- 信号除噪
- 趋势分析和预测
- 检测数据中的突然、不连续、变化或异常行为等
- 压缩大数据
- 如JPEG2000的新图像压缩标准完全基于小波
- Data encryption, i.e. secure the data
- 与机器学习相结合,提高建模精度
2. 几个实例
(1)除噪和趋势分析
A very good example of using wavelet transform for noise removal is one of my paper [1]. We use approximation instead of the original signal for modelling (or machine learning) because the original data is noisy. For example, we use the approximation (the red line) to replace the original by removing the high frequency signals (or noise).
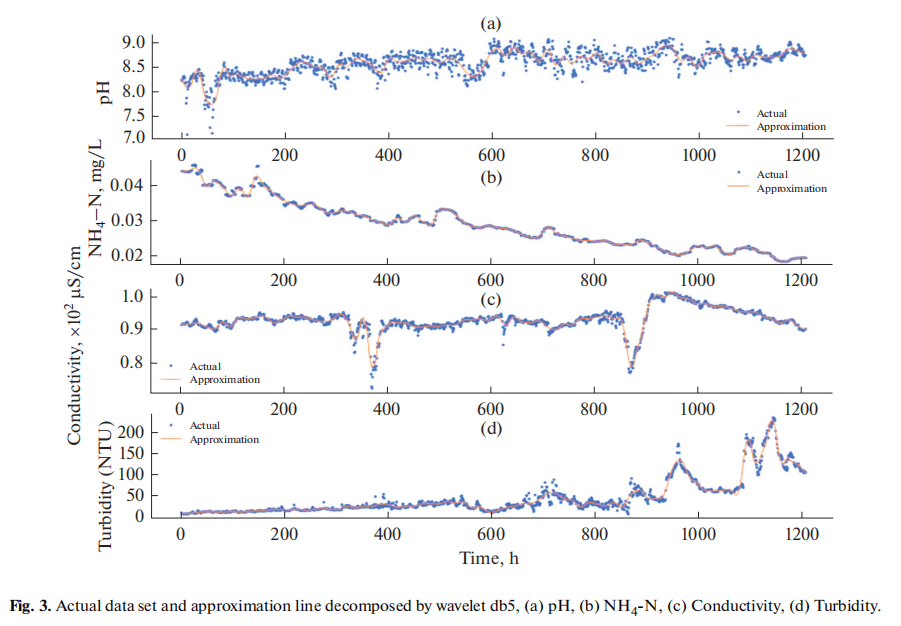
(2)不连续性,异常变化检测
For the following example, we can use wavelet transform to find abrupt discontinuities and abnormal changes.
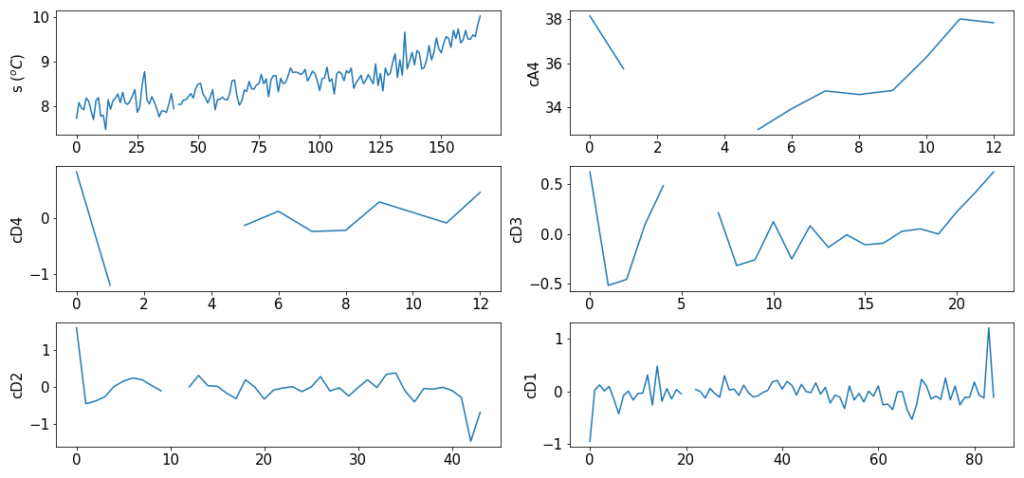
(3)增加模型的准确度
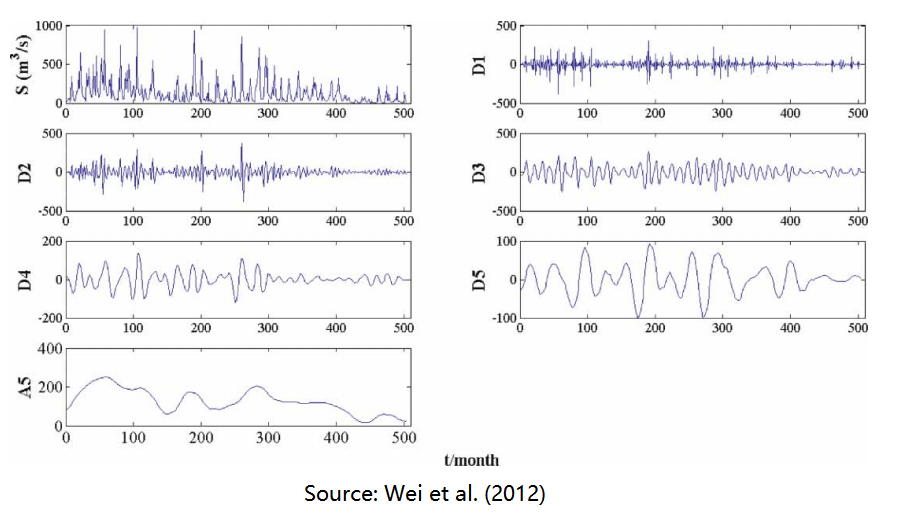
I also published 3 paper about how to model the approximation and details separately, and then predict the approximation and detail(s) . Finally, we can obtain the prediction of the original by reconstructing predictions of the approximation and detail(s).
(4)图像压缩
Another example is applying wavelet transforms for big data or image compression. The new image compression standard called JPEG2000 is fully based on wavelets. From the following example, it illustrates that the image (my photo) is compressed by more than half. The original image is 32.5 Kb, while the compressed on using wavelet transforms has only 15.1Kb.

3. Online Course
如果你有兴趣从基础学习实用小波变换,欢迎参加以下课程:实用Python小波变换(II):一维离散小波变换参考文献:
[1] Yuan, M., Wei, S., Sun, M., & Zhao, J. (2022). Wavelet Decomposition and Seq2Seq Hybrid Models for Water Quality Prediction. Water Resources, 49(4), 743-752.
[2] Wei, Shouke, Depeng Zuo, and Jinxi Song. “Improving prediction accuracy of river discharge time series using a Wavelet-NAR artificial neural network.” Journal of Hydroinformatics 14, no. 4 (2012): 974-991.
